07 정렬 알고리즘 - 힙 정렬 (Heap Sort)
힙 정렬 (Heap Sort)
▶힙 정렬은 힙 자료구조를 기반으로 원소들을 정렬하는 방식을 의미합니다. 힙에 대한 기본 지식은http://lktprogrammer.tistory.com/69 에서 확인 할 수 있습니다.
■ 정렬 과정
▶ 이번 게시글에서는 최대힙을 기준으로 설명을 하겠습니다. 힙의 기본은 완전 이진 트리의 형태이면서 부모 노드가 자식 노드보다 큰 값을 가지는 힙 성질을 만족하는 트리를 의미합니다. 따라서 최상위 노드인 루트 노드는 전체 원소 중에서 항상 최대값을 가지게 됩니다.
1. 배열에 저장 된 원소들을 최대힙으로 구성
2. 루트 노드에 존재하는 값을 가지고 오고, 가장 말단에 있는 노드를 루트 노드에 위치 시킵니다. 새로 자리 잡은 루트 노드에 대하여 다시 힙 성질에 맞게끔 배열을 조정합니다. (DownHeap 과정)
3. 배열에 남아 있는 원소가 없을때까지 2번 과정을 반복합니다.
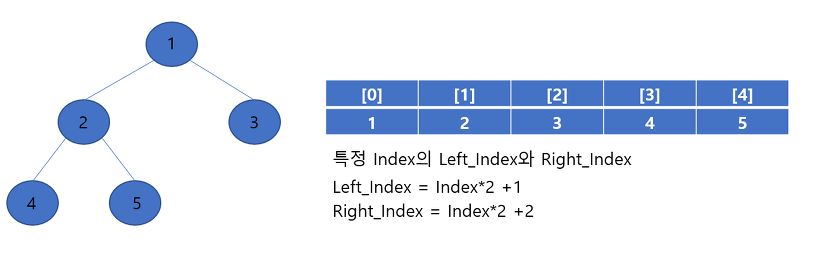
▶ 다음과 같은 배열 {1,2,3,4,5}에 대하여 반대로 내림차순으로 정렬하는 과정을 살펴 보겠습니다. 먼저 특정 인덱스 i에 대한 왼쪽 자식 노드의 인덱스는 i*2+1에 해당되며 오른쪽 자식 노드는 i*2+2에 해당 됩니다. (인덱스가 0에서부터 시작하는 경우)
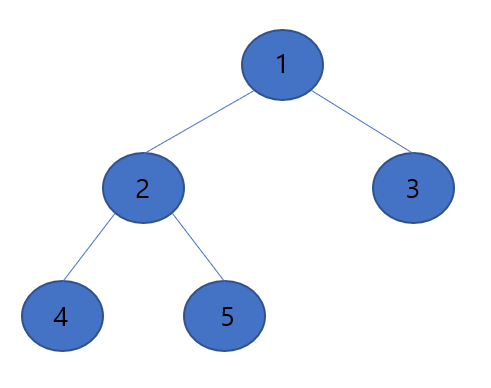
▶먼저 현재 트리의 경우는 힙이 아닙니다. 먼저 최대힙 성질을 만족하도록 트리를 조정해야 합니다. 가장 말단 노드부터 시작하여 특정 노드가 루트노드가 되는 서브 트리가 힙성질을 만족하게 되면 최종적으로 전체 트리가 힙 성질을 만족 할 수 있습니다. 실제로는 가장 말단에 있는 5부터 시작하여야 하지만 5의 경우에는 리프 노드로 자식 노드가 존재하지 않습니다. 즉 자식 노드를 가지고 있는 레벨의 노드부터 시작을 하면 됩니다. 자식 노드를 가지는 레벨의 시작 인덱스는 전체 노드의 개수/2가 되고 위 그림에서는 5/2=2인 2번 인덱스인 3부터 시작을 합니다.
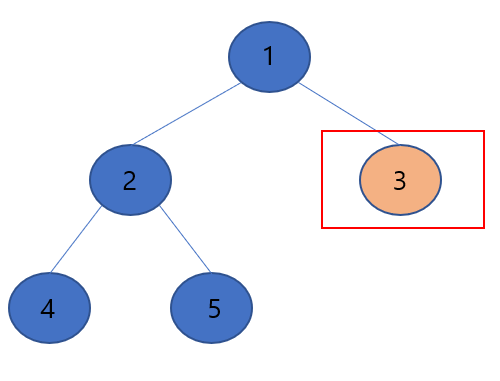
▶3을 루트노드로하여 힙 성질을 만족하도록 바꿉니다. 그런데 3은 자식 노드가 없으므로 힙 성질을 만족한다고 생각하고 넘어갑니다.
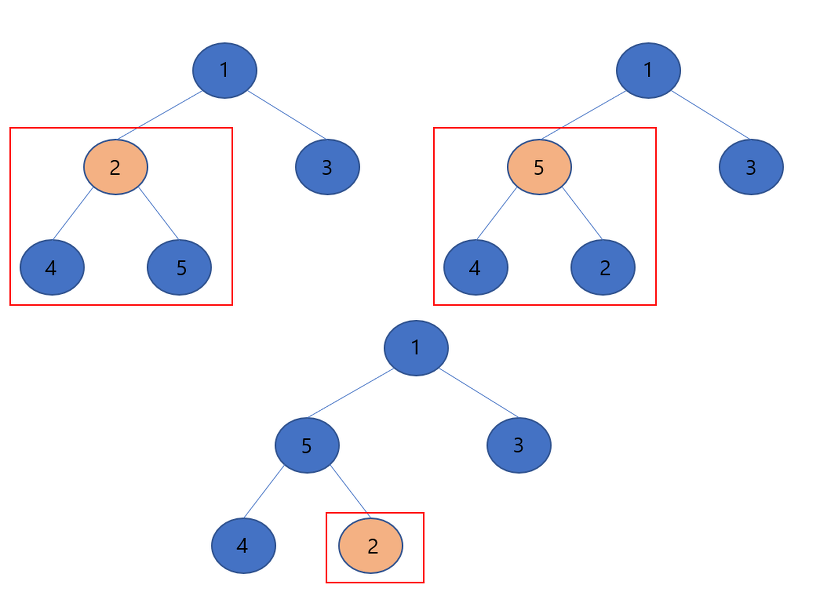
▶다음은 2를 루트 노드로 하는 서브 트리를 힙으로 만드는 과정입니다. 자식 노드인 4와 5중에서 큰 값인 5와 2를 비교를 합니다. 5과 더 크므로 2와 5를 자리를 바꿉니다. 그리고 위치가 바뀐 노드를 루트 노드로 하는 서브 트리를 힙으로 조정 할려고 하니 자식 노드가 존재하지 않습니다.
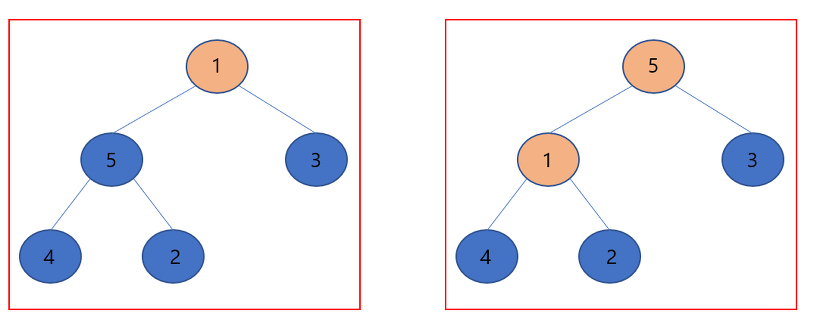
▶마지막으로 1에 대하여 힙 성질을 만족하도록 조정합니다. 두 자식 노드 중 큰 값 5과 1보다 크므로 두 위치를 교환합니다.
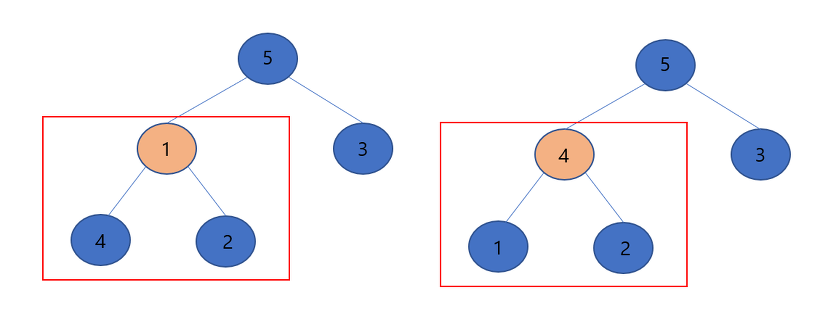
▶마지막으로 위치가 바뀐 노드를 루트 노드로 하는 서브트리를 최대힙을 만족하도록 조정합니다. 최상위 노드인 1은 두 자식 노드중 큰 값 4보다 작으므로 둘의 위치를 교환합니다. 바뀐 노드 1를 루트 노드로 하는 서브 트리를 힙 성질이 만족하다록 조정할려고 하니 자식 노드가 존재하지 않으므로 여기까지 합니다.
여기까지 완료가 되었다면 힙이 완성 됩니다. 이제 실제로 DownHeap 과정을 반복하면서 정렬된 데이터 값을 가지고 오는 부분을 살펴 보겠습니다.

▶루트 노드의 값 5를 가지고 오고 가장 말단에 있는 노드 2를 루트 노드에 위치 시킵니다. 그런 다음 다시 루트노드에 대하여 최대 힙 성질을 만족하도록 배열을 조정합니다. 4과 2보다 크므로 둘의 위치를 교환합니다. 그런 다음바뀐 위치의 노드2에 대하여 최대 힙 성질을 만족하도록 조정합니다. 2가 1보다 크므로 그대로 두게 됩니다.
이런식으로 힙에서 루트 노드를 가지고 오고 말단 노드를 루트 노드에 위치 시키고 최대힙을 구성하는 것을 반복함으로써 힙 정렬을 시도하게 됩니다.
■ 힙 정렬 구현
public class Heap {
private int Heap_Size;
private int data[];
public Heap(int[] data,int Heap_Size) //정렬하고자 하는 배열과 크기를 저장합니다.
{
this.Heap_Size = Heap_Size;
this.data = data;
}
public void Heap_Sort()
{
for(int i=Heap_Size/2;i>=0;i--) //최초 배열을 최대힙으로 구성합니다.전체 원소의
{
Max_Heapfiy(i);
}
for(int i=0;i<data.length;i++) //DownHeap을 반복하며 정렬된 결과를 출력합니다.
{
System.out.println(DownHeap());
}
}
public void Max_Heapfiy(int i)
{
int left_node= i*2+1; //왼쪽 자식 노드의 인덱스
int right_node = i*2+2; //오른쪽 자식 노드의 인덱스
int Max; //부모 노드와 자식 노드중 큰 값을 가지는 노드의 인덱스
if(left_node < Heap_Size) //왼쪽 자식 노드가 존재하는 경우
{
if(data[left_node]>data[i]) //왼쪽 자식 노드가 부모 노드보다 큰 경우
{
Max = left_node;
}
else //왼쪽 자식 노드가 부모 노드보다 작은 경우
{
Max = i;
}
}
else //왼쪽 자식 노드가 없으면 return
{
return;
}
if(right_node < Heap_Size) //오른쪽 자식 노드가 있는 경우
{
if(data[right_node]>data[Max]) //오른쪽 자식 노드가 왼쪽 자식 노드와 부모 노드보다 큰 경우
{
Max = right_node;
}
}
if(Max != i) //기존 부모노드보다 큰 값이 자식 노드에 있는 경우
{
Swap(Max,i);
Max_Heapfiy(Max);
}
}
public int DownHeap()
{
int max = data[0]; //루트 노드를 저장
data[0] = data[--Heap_Size]; //말단 노드를 루트 노드에 위치 시키고 힙의 크기를 --
Max_Heapfiy(0); //루트 노드에 대한 최대힙화
return max;
}
public void Swap(int Max,int i)
{
int tmp = data[Max];
data[Max] = data[i];
data[i] = tmp;
}
}
출처 : https://lktprogrammer.tistory.com/70?category=672214
'기타 정보 > 알고리즘' 카테고리의 다른 글
| [자바 프로그래밍] 재귀(Recursion) 알고리즘 기초 (0) | 2021.12.13 |
|---|---|
| 06 정렬 알고리즘 - 기수 정렬(Radix Sort) (0) | 2021.12.13 |
| 05 정렬 알고리즘 - 병합 정렬 (Merge Sort) (0) | 2021.12.13 |
| 04 정렬 알고리즘 - 퀵 정렬 (Quick Sort) (0) | 2021.12.13 |
| 03 정렬 알고리즘 - 버블 정렬 (Bubble Sort) (0) | 2021.12.13 |
| 02 정렬 알고리즘 - 삽입 정렬 (Insetion Sort) (0) | 2021.12.13 |
| 01 정렬 알고리즘 - 선택 정렬(Selection Sort) (0) | 2021.12.13 |
| [알고리즘] 분할정복 방법 - 이진 탐색, 퀵 정렬 알고리즘 (0) | 2021.04.21 |