05 힙(Heap) 자료구조
힙 자료구조
힙 자료구조는 원소 값들 중에서 최대값과 최소값을 구하는데 효율적인 자료 구조를 의미합니다.
트리의 개념을 공부하고 싶으면
04 트리와 이진트리 (Tree & Binary Tree) 기본
여기를 참조해주세요.
힙은 완전 이진 트리의 형태를 가지면서 동시에 다음과 같은 힙 성질을 만족해야 합니다.
● 부모노드가 자식노드보다 큰 경우 - 최대 힙
● 부모노드가 자식노드보다 작은 경우 - 최소 힙
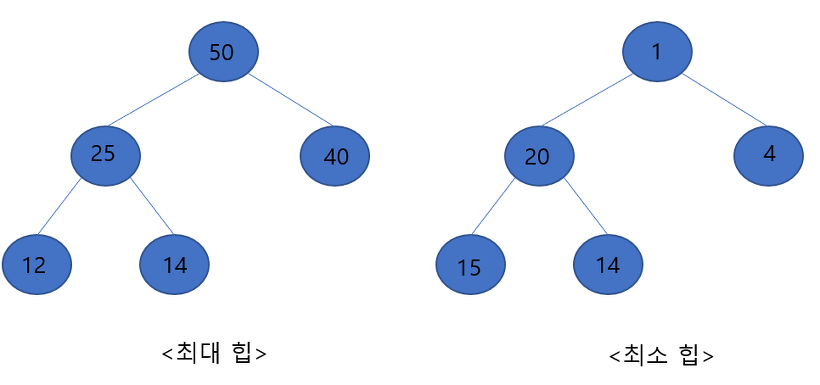
▶ 이번 게시글에서는 최대 힙을 기준으로 설명 하겠습니다. 왼쪽 최대 힙을 보면 모두 부모 노드의 값이 자식 노드 값보다 큰 형태를 이루고 있습니다. 부모 노드 50의 경우 자식 노드 25와 40보다 크며, 부모 노드 25는 자식 노드 12와 14보다 큰 형태를 이루고 있습니다. 즉, 힙의 이러한 성질 때문에 루트 노드는 힙에서 가장 큰 값이 위치가 됩니다.
■ UpHeap
▶UpHeap은 힙에 새로운 원소를 삽입하고, 새로운 원소를 포함한 새로운 힙을 구성하는 과정을 의미합니다. 과정은 새로 추가되는 원소를 가장 말단에 위치를 시키고, 부모 노드와 값을 비교하여 부모 노드보다 값이 클 경우 위치를 교환하는 방식입니다. 이 과정을 자신이 루트 노드까지 위치하거나 부모 노드보다 작을 때 까지 반복하게 됩니다. 위에 그림 왼쪽의 최대 힙에 60을 추가하는 모습을 살펴 보겠습니다.
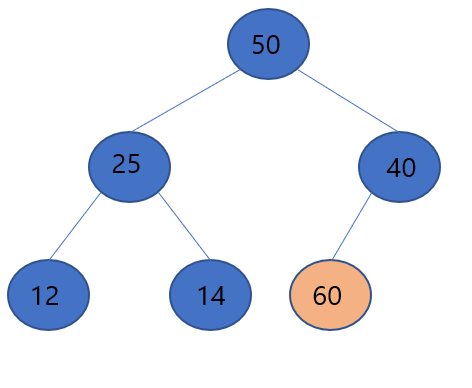
▶먼저 가장 말단에 값이 60인 노드를 추가하게 됩니다.

▶ 부모노드인 40과 비교하여 60이 더 크므로 둘의 위치를 교환합니다.
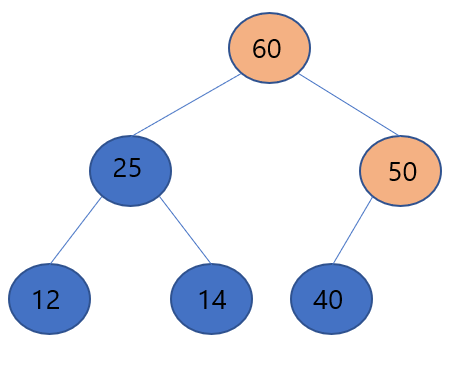
▶ 이번엔 교환 된 위치에서의 부모노드인 50과 비교하여 60이 더 크므로 둘의 위치를 교환합니다. 삽입 된 60이 루트 노드에 위치하므로 UpHeap의 과정은 여기서 멈추게 되고 최종적으로 힙의 형태를 유지하게 됩니다.
■DownHeap
▶ DownHeap은 UpHeap과는 반대로 힙에서 노드를 제거하는 작업을 의미합니다. 즉 힙의 루트로부터 최대값을 가져오는 일을 의미합니다. 그런 다음 다시 힙을 유지해야 하므로 DownHeap 과정을 거치게 됩니다. 가장 먼저 루트값이 비게 되므로 가장 말단에 있는 값을 루트 노드에 위치 시킨 다음 자식 노드와 비교를 하여 자식 노드보다 클 경우에는 그대로 유지시키고 작을 경우 자식 노드와 위치를 교환합니다. 이 과정을 자신이 리프 노드가 되거나 자식 노드보다 자신이 클 경우까지 반복을 하게 됩니다. 위 60이 추가 된 힙에 대하여 DownHeap을 시도하는 모습을 살펴 보겠습니다.
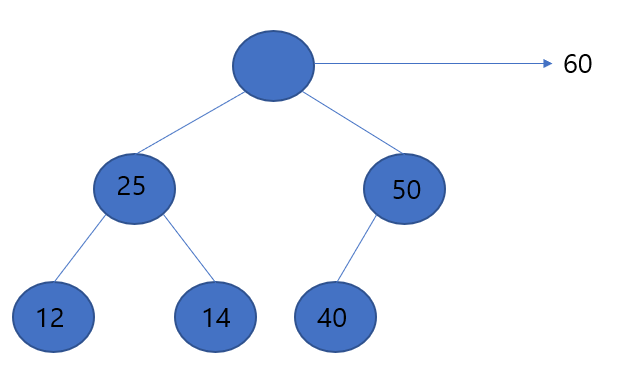
▶최대 값에 속하는 루트 노드의 값을 가지고 옵니다. 말단 노드인 40을 루트 노드에 위치 시킵니다.
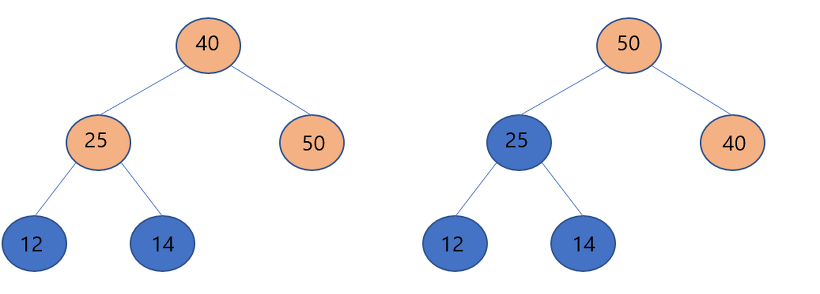
▶말단 노드인 40을 루트 노드로 위치시키고 두 자식 노드에 대하여 비교를 실시 합니다. 두 자식 노드 중에서 더 큰 노드를 구하여 40과 비교를 실시합니다. 즉, 25와 50중 50이 더 크므로 50이 부모노드인 40과 비교 대상이 됩니다. 50이 더 크므로 둘의 위치를 교환하게 됩니다. 다시 40에 대하여 자식 노드를 비교 할려고 하지만 더 이상 자식 노드가 존재하지 않으므로 DownHeap을 마무리 하게 됩니다.
■ 힙을 배열로 표현하기
▶ 힙을 완전 이진 트리로 구성되기 때문에 배열을 통해서 구성합니다.
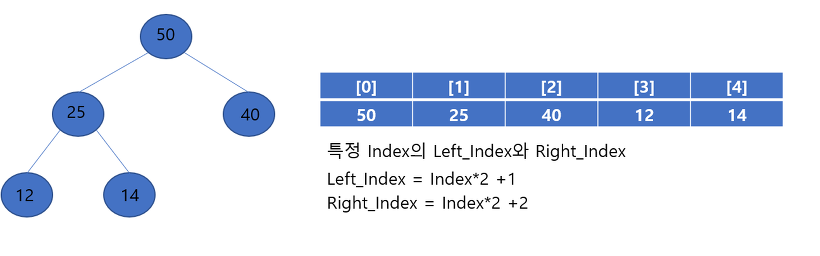
▶특정 Index에 대하여 두 자식 노드의 index를 구하는 공식은 다음과 같습니다. 즉 25값을 가지는 1번 인덱스 노드에 대하여 left_index는 1*2+1인 3번 인덱스에 해당되며 right_index의 경우에는 1*2+2인 4번 노드에 해당이 됩니다.
다음 포스팅에서는 힙을 사용하여 원소들을 정렬하는 방법과 실제 구현에 대하여 포스팅 하도록 하겠습니다.
출처 : https://lktprogrammer.tistory.com/69?category=676210
'기타 정보 > 자료구조' 카테고리의 다른 글
| 04 트리와 이진트리 (Tree & Binary Tree) 기본 (0) | 2021.12.15 |
|---|---|
| 03 원형 큐 (Circular Queue) 자료 구조 (0) | 2021.12.13 |
| 02 선형 큐 (Linear Queue) 자료구조 (0) | 2021.12.13 |
| 01 스택 (Stack) 자료 구조 (0) | 2021.12.13 |
| [자료구조] Java 삽입정렬 (insertion sort) 정리 (0) | 2019.08.06 |
| [자료구조] Java 선택정렬 (Selection Sort) 정리 (0) | 2019.08.06 |
| [자료구조] Java 해쉬(Hash) 기본 개념과 구조 (분리연결법) (0) | 2019.08.06 |
| [자료구조] Java 원형 큐(Circular Queue), 우선순위 큐(Priority Queue), 데크(Deque-double ended queue) (0) | 2019.08.06 |